Introduction:
Quantum computing represents a paradigm shift in computation, promising to revolutionize industries, tackle complex problems, and accelerate scientific discovery. At the heart of this technological marvel lie quantum algorithms, the fundamental building blocks that exploit the unique properties of quantum mechanics to perform computations. In this article, we embark on a journey through the intricacies of quantum computing algorithms, unraveling their significance, exploring their applications, and understanding their inner workings.
Understanding Quantum Computing:
Before delving into quantum algorithms, it’s crucial to grasp the basic principles of quantum computing. Classical computers use bits as the smallest unit of information, represented as either 0 or 1. In contrast, quantum computers leverage quantum bits or qubits, which can exist in superposition, representing both 0 and 1 simultaneously. Moreover, qubits can be entangled, allowing for the creation of complex quantum states.
Quantum Computing Algorithms:
Quantum algorithms are tailored to harness these quantum phenomena to solve computational problems more efficiently than their classical counterparts. Here are some key quantum algorithms that have garnered significant attention:
- Grover’s Algorithm: Grover’s algorithm addresses the problem of unstructured search, where the goal is to find a specific item in an unsorted database. Classically, this task requires checking each item individually, resulting in a time complexity of O(N). However, Grover’s algorithm achieves quadratic speedup, with a time complexity of O(√N), making it exponentially faster for large datasets.
- Shor’s Algorithm: Shor’s algorithm is a groundbreaking algorithm for integer factorization, a problem notoriously difficult for classical computers. It efficiently factors large numbers into their prime components, a task of paramount importance in cryptography. Shor’s algorithm demonstrates exponential speedup over classical algorithms, posing a significant threat to current cryptographic systems relying on the difficulty of integer factorization.
- Quantum Fourier Transform (QFT): The Quantum Fourier Transform is a quantum analog of the classical Fourier transform, which decomposes a signal into its frequency components. QFT plays a crucial role in various quantum algorithms, including Shor’s algorithm, where it enables the efficient computation of modular exponentiation.
- Quantum Phase Estimation (QPE): Quantum Phase Estimation is a key subroutine used in many quantum algorithms, particularly in quantum chemistry and quantum simulation. It allows for the estimation of eigenvalues and eigenvectors of unitary operators, enabling precise predictions of quantum systems’ behavior.
- Variational Quantum Eigensolver (VQE): VQE is a hybrid quantum-classical algorithm designed for finding the ground state energy of a given Hamiltonian, a task with numerous applications in chemistry and material science. VQE combines quantum circuits with classical optimization techniques, making it suitable for near-term quantum devices.
Applications of Quantum Algorithms:
Quantum algorithms hold immense potential across various domains, including:
- Cryptography: Shor’s algorithm threatens the security of widely-used cryptographic schemes such as RSA and ECC, driving the need for post-quantum cryptographic solutions.
- Optimization: Quantum algorithms offer significant speedup for optimization problems, ranging from logistics and supply chain management to portfolio optimization in finance.
- Machine Learning: Quantum machine learning algorithms leverage quantum principles to enhance data processing, pattern recognition, and optimization tasks, promising advancements in AI and data analytics.
- Drug Discovery: Quantum algorithms enable accurate simulations of molecular structures and interactions, expediting drug discovery and development processes.
- Financial Modeling: Quantum algorithms facilitate faster and more accurate risk assessment, portfolio optimization, and option pricing in financial markets.
Challenges and Future Directions:
Despite the tremendous promise of quantum algorithms, several challenges hinder their widespread adoption:
- Error Correction: Quantum computers are highly susceptible to errors due to decoherence and noise. Developing robust error correction techniques is essential to ensure the reliability of quantum computations.
- Scalability: Scaling quantum algorithms to large problem sizes remains a formidable challenge, requiring advances in hardware, software, and algorithmic techniques.
- Hardware Constraints: Current quantum hardware suffers from limitations such as qubit connectivity, coherence times, and gate fidelities, necessitating ongoing research to overcome these constraints.
- Algorithmic Innovation: Continued exploration and development of novel quantum algorithms tailored to specific applications are crucial for realizing the full potential of quantum computing.
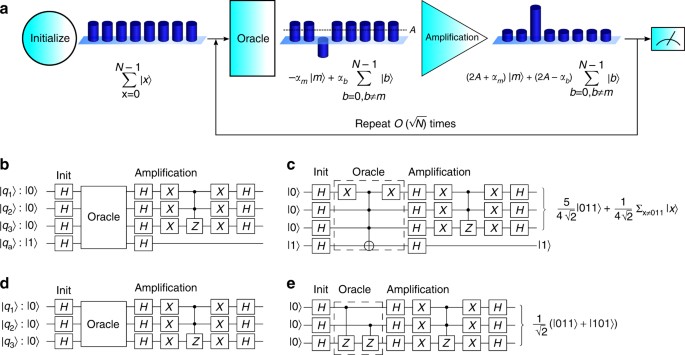
Conclusion:
Quantum computing algorithms represent the cornerstone of quantum computation, offering unprecedented capabilities to tackle complex problems across various domains. As researchers and engineers continue to push the boundaries of quantum technology, the development and refinement of quantum algorithms will play a pivotal role in unlocking the transformative power of quantum computing. While significant challenges lie ahead, the promise of quantum algorithms to revolutionize computation and scientific discovery remains as compelling as ever.