Introduction

In the realm of cutting-edge technology, quantum computing stands as one of the most revolutionary fields with the potential to redefine the limits of computation. Unlike classical computers, which rely on classical bits to process information, quantum computers employ quantum bits or qubits, leveraging the principles of quantum mechanics. This article delves into the foundational aspects of quantum computing, introducing key concepts and shedding light on its significance.
Classical vs. Quantum Computing: A Brief Overview

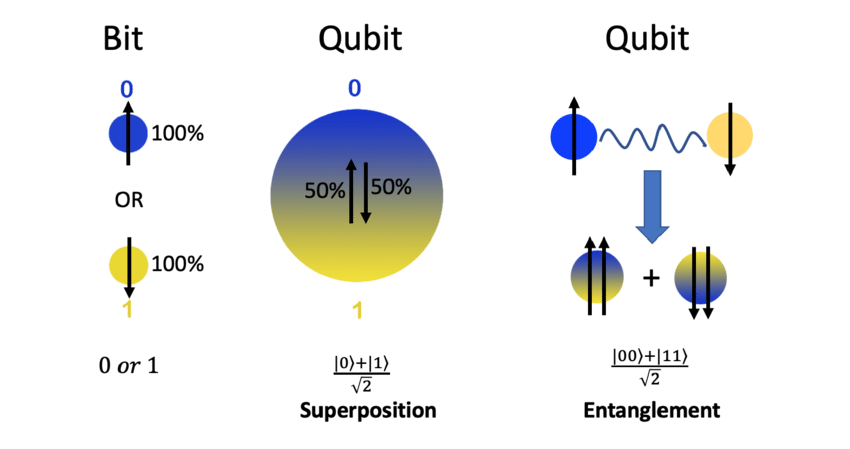
Classical computing, as we know it, operates on bits, the fundamental units of classical information. A bit can exist in one of two states: 0 or 1. Through logical operations, classical computers manipulate these bits to perform computations. While classical computing has propelled technological advancements over the past decades, certain computational problems, such as factoring large numbers or simulating quantum systems, remain challenging due to the limitations of classical algorithms.
Quantum computing, on the other hand, capitalizes on the principles of quantum mechanics to process information. At its core are qubits, which, unlike classical bits, can exist in multiple states simultaneously, thanks to a phenomenon called superposition. Moreover, qubits can be entangled, exhibiting correlations that defy classical intuition. These unique properties enable quantum computers to tackle complex problems more efficiently than classical counterparts, making them a promising avenue for breakthroughs in various domains.
Superposition and Qubits

Superposition lies at the heart of quantum computing and represents one of its most profound concepts. In classical computing, a bit can only be in one state at a time—either 0 or 1. In contrast, a qubit can exist in a superposition of both states simultaneously. This means that before measurement, a qubit can represent both 0 and 1 with certain probabilities, expanding the computational possibilities exponentially.
Mathematically, a qubit’s state can be represented as:
∣�⟩=�∣0⟩+�∣1⟩∣ψ⟩=α∣0⟩+β∣1⟩
where �α and �β are complex numbers representing the probability amplitudes of the qubit being in states ∣0⟩∣0⟩ and ∣1⟩∣1⟩, respectively. The magnitude of �α and �β determines the probability of measuring the qubit in the corresponding state upon measurement.
Entanglement
Entanglement is another fundamental concept in quantum computing, describing a phenomenon where the states of multiple qubits become correlated in such a way that the state of one qubit instantaneously influences the state of another, regardless of the distance separating them. This phenomenon, famously referred to as “spooky action at a distance” by Einstein, has been experimentally verified and forms the basis for various quantum protocols and algorithms.
Entanglement enables quantum computers to perform parallel computations and manipulate information in ways classical computers cannot. Harnessing entanglement, quantum algorithms can achieve computational speedups by exploiting interconnected qubits to process information more efficiently.
Quantum Gates and Operations
Similar to classical computers, which employ logic gates to perform operations on bits, quantum computers utilize quantum gates to manipulate qubits. However, quantum gates operate on the principles of quantum mechanics and can thus execute operations like superposition and entanglement.
Common quantum gates include the Hadamard gate, which creates superposition, the CNOT (controlled-NOT) gate, which entangles qubits, and various phase gates that introduce phase shifts. By combining these gates, quantum algorithms can perform complex computations efficiently, offering solutions to problems that are intractable for classical computers.
Quantum Algorithms and Applications
Quantum computing holds promise across diverse fields, from cryptography and optimization to drug discovery and materials science. Shor’s algorithm, for instance, exploits quantum parallelism to efficiently factor large numbers, posing a threat to classical cryptographic schemes like RSA. Grover’s algorithm, on the other hand, accelerates the search of an unsorted database quadratically faster than classical algorithms, offering implications for optimization problems.
In addition to these well-known algorithms, ongoing research continues to explore new quantum algorithms and their applications across various domains. Machine learning, finance, and quantum chemistry are among the areas poised to benefit from advancements in quantum computing, paving the way for transformative technologies and scientific discoveries.
Conclusion
Quantum computing represents a paradigm shift in computation, leveraging the principles of quantum mechanics to transcend the limitations of classical computing. By harnessing phenomena like superposition and entanglement, quantum computers offer the potential to solve complex problems exponentially faster than classical counterparts. While quantum computing is still in its nascent stages, ongoing research and development promise to unlock its full potential, ushering in a new era of computation and innovation. Understanding the fundamentals of quantum computing is essential for grasping its implications and navigating the frontier of this groundbreaking field.